Relearning the Metropolis-Hastings Algorithm

Markov Chain Monte Carlo (MCMC) is a family of methods for efficiently sampling from an arbitrary probability distribution. The Metropolis-Hastings algorithm is a specific example of MCMC, which we’ll be summarizing in this post. First, however, let’s justify the need of these sampling algorithms.

Sampling is hard, sometimes

Informally, the problem of sampling a distribution is usually posed as:

• We are given some black-box algorithm for generating uniformly random numbers from the interval $[0, 1)$, which we can use as many times as we like.
• We are given some function $f(X)$ which we call a probability distribution, where the integral of $f$ over the entire domain $X$ is equal to $1$.
• Using these, we want to create an algorithm such that the distribution of samples generated by this algorithm approximates $f$ arbitrarily close as the number of samples increase.. For example, suppose we want to generate random samples from the normal distribution $\mathcal{N}(0, 1)$. We’re able to use the Box-Muller Transform to come up with a sampling method:
  1. Generate random numbers $U_1$ and $U_2$ from the uniform distribution on $[0, 1)$.
  2. Output $Z = \sqrt{-2 \ln U_1}\cos (2\pi U_2)$. Using only our black-box algorithm for generating random numbers between 0 and 1, we’re able to produce an algorithm where the probability distribution of $Z$ equals the normal distribution.

Rejection sampling

In the previous example, we had a nice, clean sampling method which resulted from the mathematical properties of the normal distribution. However, this isn’t always the case – consider, for example, the normal distribution $x \sim \mathcal{N}(0, 1)$ with the additional condition that the value $x$ must be at least 1. We’re no longer able to directly use the Box-Muller Transform, but there’s a way to get around this:

1. Use the Box-Muller Transform to sample a value $Z \sim \mathcal{N}(0, 1)$.
2. If $Z \ge 1$, output $Z$. Otherwise, return to Step 1. This method of sampling a wider distribution, then accepting or rejecting samples based on a condition, is known as Rejection sampling. While rejection sampling methods always require a non-deterministic amount of time, rejection sampling is often fast and simple, and as a result is frequently useful for sampling conditional distributions.

Now consider the normal distribution $x \sim \mathcal{N}(0, 1)$, except with the additonal condition that the value $x$ must be at least 5. Given a single sample of the normal distribution, the probability that the condition holds true is about 1 in 5 million. As a result, using rejection sampling in the same fashion as the previous example isn’t viable, since it’s too costly in terms of runtime. This is where MCMC methods come in.

The Metropolis-Hastings algorithm

The Metropolis-Hastings algorithm is able to sample an arbitrary probability distribution $f$ given access to two things:

1. The previously mentioned $[0, 1)$ uniform distribution sampler
2. A function $g$ proportional to the distribution $f$.

Using the $(0, 1]$ sampler, we also need to supply the algorithm with a sampling method for some distribution $h(x \vert y)$, where $h$ is symmetric: $h(x \vert y) = h(y \vert x)$. One commonly used distribution (which we’ll be using) is $h(x \vert y) = \mathcal{N}(y, 1)$. Now that we specified everything that we need, the Metropolis-Hasting algorithm, as taken from Wikipedia, works as follows:

1. Pick some element $x$ to be a starting point.
2. Sample a candidate $x^{\prime}$ from the distribution $h(x^{\prime} \vert x)$.
3. Calculate the acceptance ratio $\alpha = g(x^{\prime}) / g(x)$.
4. Generate a random number $u$ from the uniform distribution on $[0, 1)$. a. If $u \le \alpha$, $x^{\prime}$ becomes the newest sample: append $x^{\prime}$ to the list of samples and set $x = x^{\prime}$. b. If $u > \alpha$, nothing happens.
5. Return to Step 2.

A few things are worth noting: the latest sample $x^{\prime}$ is always accepted when $g(x^{\prime}) \ge g(x)$ and $\alpha \ge 1$. As a result, the value $x$ tends to move towards higher-probability regions. In addition, the Metropolis-Hastings algorithm is often called a random walk MCMC due to how $x$ randomly changes in direction every iteration. Finally, the initial choice of starting point and choice of $h$ greatly affects how many iterations we need to closely approximate $f$. For example, in our previous distribution of $x \sim \mathcal{N}(0, 1)$ and $x \ge 5$, the combined choice of starting point $x = 0$ and distribution $h(x \vert y) = \mathcal{N}(y, 1)$ would require multiple iterations before the algorithm finally reaches a point where $g(x)$ is nonzero.

There’s another problem with Metropolis-Hastings: consider the distribution $\mathcal{N}(0, 1)$ with the additional condition $\vert x \vert > 100$. Without a sufficiently high-variance choice of distribution $h$, the algorithm will be forever stuck in one of the two disjoint areas of nonzero probabilities. As a result, it’s pretty difficult for Metropolis-Hastings to accurately sample this entire distribution without manual modifications.

Implementation

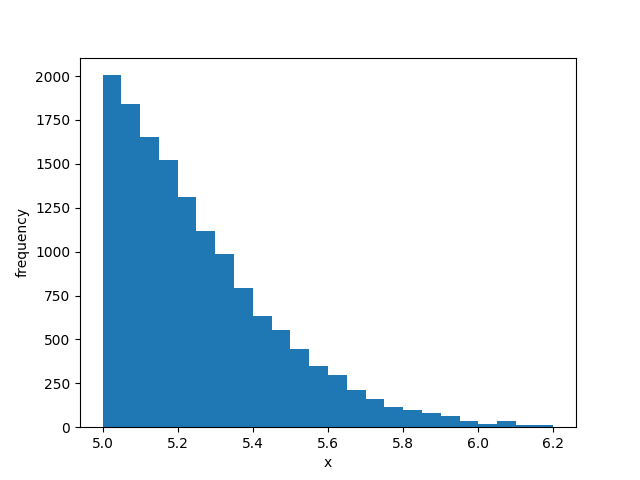
You can find my implementation of Metropolis-Hastings here, using the previously mentioned normal distribution with $x > 5$ as an example. Iterating 100,000 times, we’re able to obtain the resulting distrbution of samples: